Turunan fungsi ( diferensial ) adalah fungsi lain dari suatu fungsi sebelumnya, misalnya fungsi f menjadi f' yang mempunyai nilai tidak beraturan[1]. Konsep turunan sebagai bagian utama dari kalkulus dipikirkan pada saat yang bersamaan oleh Sir Isaac Newton ( 1642 – 1727 ), ahli matematika dan fisikabangsa Inggris dan Gottfried Wilhelm Leibniz ( 1646 – 1716 ), ahli matematika bangsa Jerman. Turunan ( diferensial ) digunakan sebagai suatu alat untuk menyelesaikan berbagai masalah dalam geometridan mekanika.
Konsep turunan fungsi secara universal banyak sekali digunakan dalam bidang ekonomi untuk menghitung biaya marjinal, biaya total atau total penerimaan, dalam bidang biologi untuk menghitung laju pertumbuhan organisme, dalam bidang fisikauntuk menghitung kepadatan kawat, dalam bidang kimia untuk menghitung laju pemisahan, dalam bidang geografi dan sosiologi untuk menghitung laju pertumbuhan penduduk dan masih banyak lagi.
Secara umum, turunan menyatakan bagaimanakah suatu besaran berubah akibat perubahan besaran yang lainnya, Contohnya: turunan dari posisi sebuah benda bergerak terhadap waktu ialah kecepatan sesaat oleh objek tersebut.
Proses dalam menemukan sebuah turunan disebut diferensiasi. Dan kebalikan dari sebuah turunan disebut dengan Anti Turunan. Teorema fundamental kalkulus mengatakan bahwa antiturunan yaitu sama dengan integrasi. Turunan dan integral ialah 2 fungsi penting dalam kalkulus.




 Ialah simbol untuk turunan pertama.
Ialah simbol untuk turunan pertama. Ialah simbol untuk turunan kedua.
Ialah simbol untuk turunan kedua. Ialah simbol untuk turunan ketiga.
Ialah simbol untuk turunan ketiga.
Simbol yang lainnya selain  dan
dan  ialah
ialah  dan
dan .
.
Pengertian Turunan Fungsi
Turunan Fungsi (diferensial) ialah fungsi lain dari suatu fungsi sebelumnya, misalkan fungsi f menjadi f’ yang memiliki nilai tidak beraturan.
Konsep turunan sebagai bagian utama dari kalkulus dipikirkan pada saat yang bersamaan oleh seorang Ilmuan Ahli matematika dan Fisika berkebangsaan inggris yaitu Sir Isaac Newto (1642 – 1727) dan Ahli matematika bangsa Jerman Gottfried Wilhelm Leibniz (1646 – 1716).
Turunan (diferensial) digunakan sebagai suatu alat untuk menyelesaikan berbagai masalah-masalah didalam bidang geometri dan mekanika.
Konsep turunan fungsi secara universal atau menyeluruh banyak sekali digunakan didalam berbagai bidang keilmuan.
Sebut saja dalam bidang ekonomi: digunakan untuk menghitung berupa, biaya total atau total penerimaan.
Dalam bidang biologi: digunakan untuk menghitung laju pertumbuhan organisme
Dalam bidang fisika: digunakan untuk menghitung kepadatan kawat,
Dalam bidangkimia: digunakan untuk menghitung laju pemisahan
Dan dalam bidang geografi dan sosiologi: digunakan untuk menghitung laju pertumbuhan penduduk dan masih banyak lagi.
Rumus Dasar Turunan dari Turunan Fungsi
Aturan-aturan dalam turunan fungsi ialah:
- f(x), menjadi f'(x) = 0
- Apabila f(x) = x, maka f’(x) = 1
- Aturan pangkat : apabila f(x) = xn, maka f’(x) = n X n – 1
- Aturan kelipatan konstanta : apabila (kf) (x) = k. f’(x)
- Aturan rantai : apabila ( f o g ) (x) = f’ (g (x)). g’(x))
Rumus-Rumus Turunan Fungsi Al Jabar
Rumus Turunan Fungsi Pangkat
Turunan Fungsi berbentuk pangkat, turunannya dapat menggunakan rumus
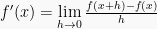
sebagai berikut:
Maka, rumus turunan fungsi pangkat ialah:
2. Rumus turunan hasil kali fungsi 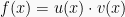
Rumusan Fungsi f(x) turunan yang terbentuk dari perkalian fungsi u(x) dan v(x), adalah:
Maka, rumus turunan fungsinya ialah:
3. Rumus turunan fungsi pembagian 
Rumus turunan fungsi pembagian dapat di tentukan dengan menggunakan rumus:
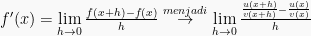
Sehingga,
Maka, rumus turunan fungsinya adalah
4. Rumus turunan pangkat dari fungsi 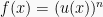
Perlu diingat, apabila

, maka:
Karna
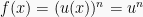
, maka:
Atau,
Maka, rumus turunan fungsinya ialah:
4. Rumus-rumus Turunan Trigonometri
Berdasarkan definisi turunan, maka dapat diperoleh rumus-rumus turunan trigonometri yakni sebagai berikut: (dengan u dan v masing-masing fungsi dari x), yakni:


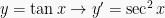

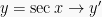
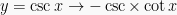

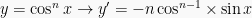


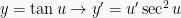
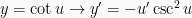
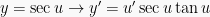
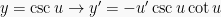


Contoh Soal dan Pembahasannya
Contoh soal 1:
Tentukanlah turunan fungsi dari f(x) = 2x(x4 – 5).
Pembahasan:
Misalkan apabila u(x) = 2x dan v(x) = x4 – 5, maka:
u‘ (x) = 2 dan v‘ (x) maka = 4x3
Dengan demikian, diperoleh penjabaran dan hasilnya:
f ‘(x) = u ‘(x).v(x) + u(x).v ’(x) = 2(x4 – 5) + 2x(4x3 ) = 2x4 – 10 + 8x4 = 10x4 – 10
Contoh ke 2: Soal Turunan Fungsi Al Jabar
Turunan fungsi pertama dari
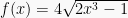
ialah:
Pembahasan:
Soal ini merupakan soal fungsi yang berbentuk y =
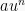
yang dapat dibahas dan diselesaikan dengan menggunakan rumus
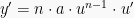
. Maka:
Sehingga turunannya yaitu:
Contoh Soal 4: Turunan Fungsi Trigonometri
Tentukan turunan pertama dari:
Pembahasan :
Untuk menyelesaikan soal ini kita dapat menggunakan rumus campuran yaitu:

dan juga
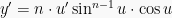
.
Maka:
Demikianlah pembahasan kita mengenai Turunan Fungsi lengkap dari pengertian hingga ke contoh soalnya.




 Ialah simbol untuk turunan pertama.
Ialah simbol untuk turunan pertama. Ialah simbol untuk turunan kedua.
Ialah simbol untuk turunan kedua. Ialah simbol untuk turunan ketiga.
Ialah simbol untuk turunan ketiga. dan
dan  ialah
ialah  dan
dan .
.
Comments
Post a Comment